As I have explained in other publications such as the Netflix Techblog, ranking is a very important part of a Recommender System. Although the Netflix Prize focused on rating prediction, ranking is in most cases a much better formulation for the recommendation problem. In this post I give some more motivation, and an introduction to the problem of personalized learning to rank, with pointers to some solutions. The post is motivated, among others, by a proposal I sent for a tutorial at this year’s Recsys. Coincidentally, my former colleagues in Telefonica, who have been working in learning to rank for some time, proposed a very similar one. I encourage you to use this post as an introduction to their tutorial, which you should definitely attend.
The goal of a ranking system is to find the best possible ordering of a set of items for a user, within a specific context, in real-time. We optimize ranking algorithms to give the highest scores to titles that a member is most likely to play and enjoy.
If you are looking for a ranking function that optimizes consumption, an obvious baseline is item popularity. The reason is clear: on average, a user is most likely to like what most others like. Think of the following situation: You walk into a room full of people you know nothing about, and you are asked to prepare a list of ten books each person likes. You will get $10 for each book you guess right. Of course, your best bet in this case would be to prepare identical lists with the “10 most liked books in recent times”. Chances are the people in the room is a fair sample of the overall population, and you end up making some money. However, popularity is the opposite of personalization. As I explained in the previous example, it will produce the same ordering of items for every member. The goal becomes is to find a personalized ranking function that is better than item popularity, so we can better satisfy users with varying tastes. Our goal is to recommend the items that each user is most likely to enjoy. One way to approach this is to ask users to rate a few titles they have read in the past in order to build a rating prediction component. Then, we can use the user’s predicted rating of each item as an adjunct to item popularity. Using predicted ratings on their own as a ranking function can lead to items that are too niche or unfamiliar, and can exclude items that the user would want to watch even though they may not rate them highly. To compensate for this, rather than using either popularity or predicted rating on their own, we would like to produce rankings that balance both of these aspects. At this point, we are ready to build a ranking prediction model using these two features.
Let us start with a very simple scoring approach by choosing our ranking function to be a linear combination of popularity and predicted rating. This gives an equation of the form score(u,v) = w1 p(v) + w2 r(u,v) + b, where u=user, v=video item, p=popularity and r=predicted rating. This equation defines a two-dimensional space as the one depicted in the following figure.
 |
Once we have such a function, we can pass a set of videos through our function and sort them in descending order according to the score. First, though, we need to determine the weights w1 and w2 in our model (the bias b is constant and thus ends up not affecting the final ordering). We can formulate this as a machine learning problem: select positive and negative examples from your historical data and let a machine learning algorithm learn the weights that optimize our goal. This family of machine learning problems is known as “Learning to Rank” and is central to application scenarios such as search engines or ad targeting. A crucial difference in the case of ranked recommendations is the importance of personalization: we do not expect a global notion of relevance, but rather look for ways of optimizing a personalized model.
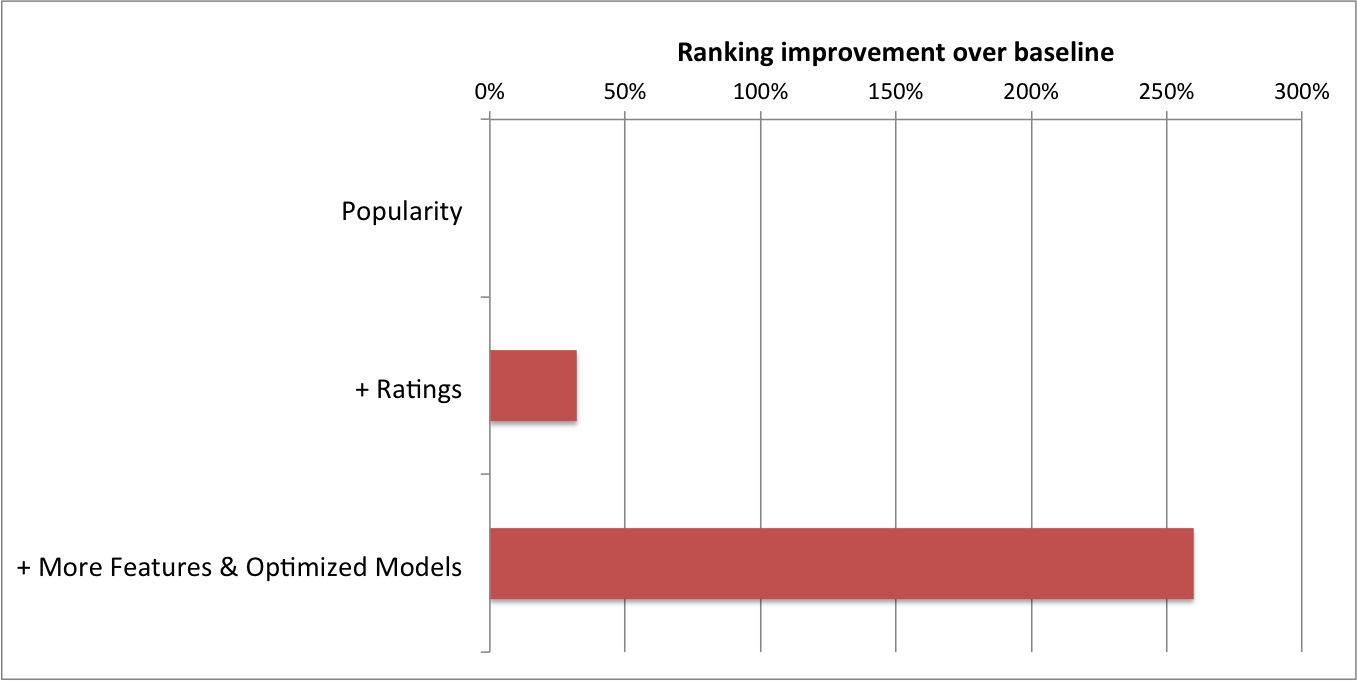
As you might guess, the previous two-dimensional model is a very basic baseline. Apart from popularity and rating prediction, you can think on adding all kinds of features related to the user, the item, or the user-item pair.Below you can see a graph showing the improvement we have seen at Netflix after adding many different features and optimizing the models.
 |
The traditional pointwise approach to learning to rank described above treats ranking as a simple binary classification problem where the only input are positive and negative examples. Typical models used in this context include Logistic Regression, Support Vector Machines, Random Forests or Gradient Boosted Decision Trees.
There is a growing research effort in finding better approaches to ranking. The pairwise approach to ranking, for instance, optimizes a loss function defined on pairwise preferences from the user. The goal is to minimize the number of inversions in the resulting ranking. Once we have reformulated the problem this way, we can transform it back into the previous binary classification problem. Examples of such an approach are RankSVM [Chapelle and Keerthi, 2010, Efficient algorithms for ranking with SVMs], RankBoost [Freund et al., 2003, An efficient boosting algorithm for combining preferences], or RankNet [Burges et al., 2005, Learning to rank using gradient descent].
We can also try to directly optimize the ranking of the whole list by using a listwise approach. RankCosine [Xia et al., 2008. Listwise approach to learning to rank: theory and algorithm], for example, uses similarity between the ranking list and the ground truth as a loss function. ListNet [Cao et al., 2007. Learning to rank: From pairwise approach to listwise approach] uses KL-divergence as loss function by defining a probability distribution. RankALS [Takacs and Tikk. 2012. Alternating least squares for personalized ranking] is a recent approach that defines an objective function that directly includes the ranking optimization and then uses Alternating Least Squares (ALS) for optimizing.
Whatever ranking approach we use, we need to use rank-specific information retrieval metrics to measure the performance of the model. Some of those metrics include Mean Average Precision (MAP), Normalized Discounted Cumulative Gain (NDCG), Mean Reciprocal Rank (MRR), or Fraction of Concordant Pairs (FCP). What we would ideally like to do is to directly optimize those same metrics. However, it is hard to optimize machine-learned models directly on these measures since they are not differentiable and standard methods such as gradient descent or ALS cannot be directly applied. In order to optimize those metrics, some methods find a smoothed version of the objective function to run Gradient Descent. CLiMF optimizes MRR [Shi et al. 2012. CLiMF: learning to maximize reciprocal rank with collaborative less-is-more filtering], and TFMAP [Shi et al. 2012. TFMAP: optimizing MAP for top-n context-aware recommendation], optimizes MAP in a similar way. The same authors have very recently added a third variation in which they use a similar approach to optimize “graded relevance” domains such as ratings [Shi et. al, “Gapfm: Optimal Top-N Recommendations for Graded Relevance Domains“]. AdaRank [Xu and Li. 2007. AdaRank: a boosting algorithm for information retrieval] uses boosting to optimize NDCG. Another method to optimize NDCG is NDCG-Boost [Valizadegan et al. 2000. Learning to Rank by Optimizing NDCG Measure], which optimizes expectation of NDCG over all possible permutations. SVM-MAP [Xu et al. 2008. Directly optimizing evaluation measures in learning to rank] relaxes the MAP metric by adding it to the SVM constraints. It is even possible to directly optimize the non-diferentiable IR metrics by using techniques such as Genetic Programming, Simulated Annealing [Karimzadehgan et al. 2011. A stochastic learning-to-rank algorithm and its application to contextual advertising], or even Particle Swarming [Diaz-Aviles et al. 2012. Swarming to rank for recommender systems].
As I mentioned at the beginning of the post, the traditional formulation for the recommender problem was that of a rating prediction. However, learning to rank offers a much better formal framework in most contexts. There is a lot of interesting research happening in this area, but it is definitely worth for more researchers to focus their efforts on what is a very real and practical problem where one can have a great impact.